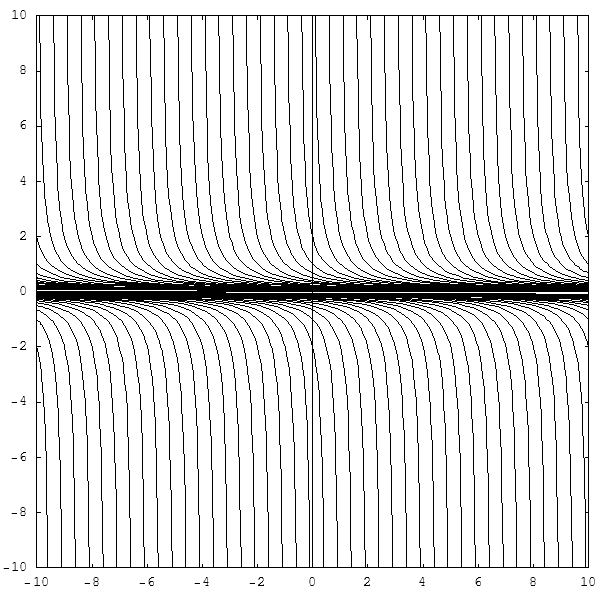
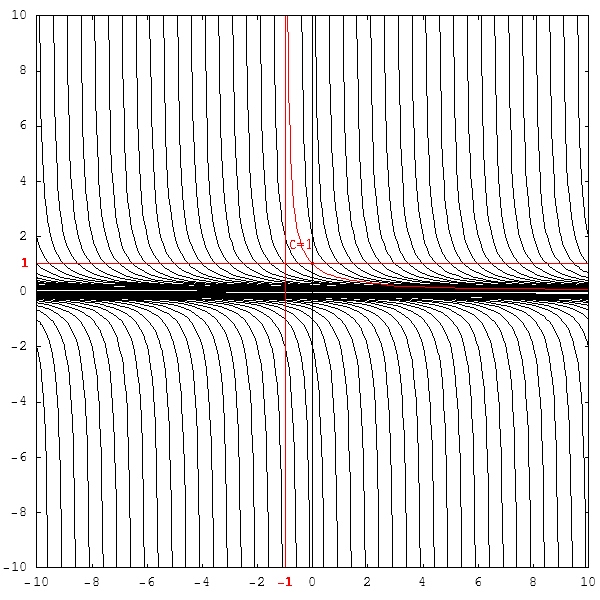
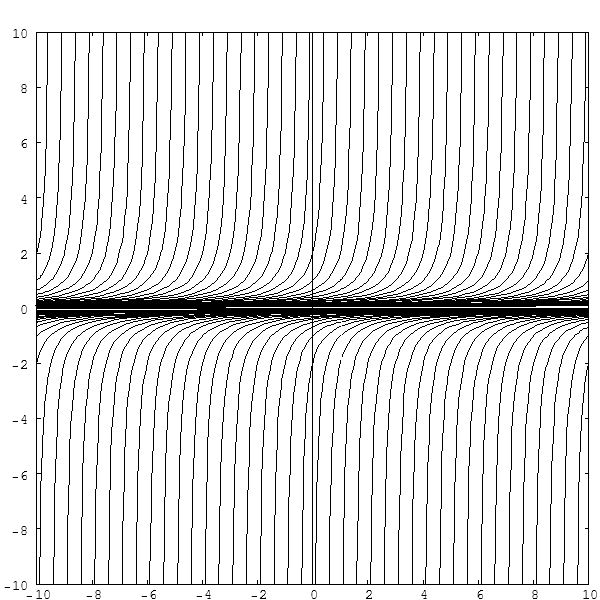
- LoVaBiLL : (Παρ Δεκ 11, 2009 8:02 pm) : "Πως ακριβώς βρίσκουμε την ισχύ (ή μη) της συνθήκης Lipschitz στην συνάρτηση y'=-y^2 , y(0)=1?"
- Πολύ ενδιαφέρον! Οπότε ανοίξαμε * και πάλι ..."Τα Κιτάπια"! - d;^) - Από αυτά που παραθέτετε λοιπόν, και κατά τη γνώμη μας, προκύπτει ότι: (1) η συνάρτηση οφείλει να είναι πραγματική συνάρτηση πραγματικής μεταβλητής, με τύπο y = y(x), (2) η y(x) οφείλει να έχει συνάρτηση πρώτης παραγώγου με τύπο y' = y'(x), και (3) οι τύποι αυτοί οφείλουν να ορίζονται -υπονοούμενα- στο μεγαλύτερο -ως προς τη σχέση διάταξης εγκλεισμού συνόλων- υποσύνολο Α του |R ή Α C |R, στο οποίο μπορούν να ισχύουν οι συνθήκες: y' = -y^2 και y(0) = 1. Αλλά τότε, επειδή από την πρώτη συνθήκη y' = y^2 προκύπτει ότι dy = -y'dx => Int{-1/y^2}dy = Int{1}dx => 1/y + C' = x + C", όπου C' και C'' αυθαίρετες σταθερές, οπότε 1/y = x + C, C = C" - C'=> y = 1/(x + C), και έτσι έπεται ότι ο γενικός τύπος για τη συνάρτηση είναι y = y(x) = 1/(x + C), C ε |R, οπότε η συνάρτηση είναι ορισμένη στο σύνολο Α = (|R - {-C}) ή, για λόγους καθαρά μαθηματικής ..."αισθητικής", αφού "το ίδιο είναι", στο σύνολο Α = (|R - {C}) ή, εν πάση περιπτώσει, στο σύνολο Α = (-οο, C) U (C, +oo), ενώ από την δεύτερη συνθήκη y(0) = 1 προκύπτει ότι 1 = 1/(0 + C) => C = 1, κι έτσι ο ειδικός, πλήρως ορισμένος, τύπος είναι εδώ y(x) = 1/(x + 1), ενώ το μεγαλύτερο υποσύνολο Α του |R, στο οποίο ορίζεται συνάρτηση y = y(x) από αυτόν τον τύπο, προκύπτει από την συνθήκη για τον παρονομαστή του τύπου αυτού: (x + 1) =/= 0 <=> x =/= -1, οπότε, δηλαδή, είναι: Α = (-οο, -1) U (-1, +οο). Και επειδή για τη συνάρτηση αυτή η παράγωγος δίδεται από τον τύπο y' = y'(x) = -1/(x + 1)^2, έπεται ότι το μεγαλύτερο υποσύνολο Α' του |R ή A' C |R, στο οποίο ορίζεται η συνάρτηση της πρώτης παραγώγου της y(x) από τον τύπο αυτόν, προκύπτει αντιστοίχως από τη συνθήκη: (x + 1)^2 =/= 0, δηλαδή το Α' είναι, προφανώς, ίδιο με το Α ή Α' = Α = (-οο, -1) U (-1, +οο). Πάμε τώρα παρακάτω; d;^) * Νικολίτσα Γιαννοπούλου * Πέτρος Ζιμουρτόπουλος
- ΥΓ - Παρακαλούμε όπως το μήνυμα αυτό παραμείνει εδώ, στα [Επιστημονικά Νέα], καθότι ναι μεν ως αφορμή έχει το θέμα [Lipschitz Condition], από τα [Μαθήματα], και παρόλο που δεν είναι Επιστημονικό "Νέο", εν τούτοις έχει για εμάς ένα γενικότερο ενδιαφέρον, επιστημονικό - d;^) -